Axis of Symmetry

The axis of symmetry is a vertical line that separates the paraballa in two equal halves. 

 

The AOS has to be written as x = h because it is the x co-ordinate in the vertex 

 

(h+k) 

 

Optimal Value 

The optimal value is a horizontal line that tells us the highest or lowest point in the

parabola. It is usually called the maximum or the minimum value in real life situations.

 

Also the Optimal Value has to be written as y= k because it is the y co-ordinate in the vertex

 

(h+k) 

 

 

NOTE: When you find the optimal value and the AOS you will acquire the Vertex 

 

Therefore in the equation y = a(x - h)² + k the - h and the k are your vertex. 

 

Transformations

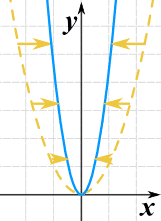
Vertical translation occurs when the y value in the vertex or when k in the

equation y = a(x - h)² + k moves up or down (increases or decreases). Yes, this

directly relates to the optimal value. 

 

If perhaps, "k" is -2 then the vertex would move two down from its orgin (0)

or if "k" is 2 then it would move two up from its origin (0)

 

Remember that this is called Vertical Translation 

 

 

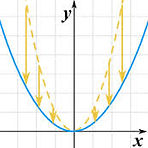
Horizontal translation is exactly what you thought. It is the oppisite of vertical 

translation and it directly relates to the AOS. This tells you when x value in the 

vertex or when - h in the equation y = a(x - h)² + k  moves to the left or right. 

 

For example, lets say that "- h" is 2 then the vertex would move two to the left 

side but if it is -2 then you would move it two to the right from the origin (0). 

 

Take note that this is called Horizontal Translation 

 

 

 

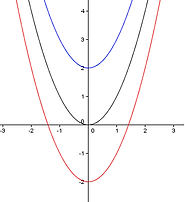
Vertical stretch is the "a" in the equation y = a(x - h)² + k as it acts towards the 

stretch or the commpression of the parabola. When "a" is greater than 1 then

the parabola seems like it is being compressed and this is true. But when the 

"a" is less than 1 then the parabola is being streched out this is a vertical stretch. 

 

Remember that a stretch in the parabola is a Vertical Strecth 

 

Remember that a compression occurs in the parabola it's called a Vertical Compression 

 

 

 

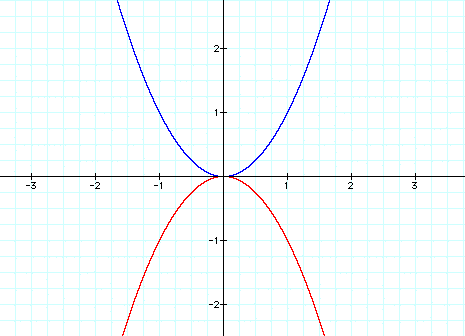
A reflection is an easy concept to remember. It is what the parabola looks like. If it is 

opening upwards then "a" is +, on the contrary when "a" is negative, we see the 

parabola open downwards. The picture on the left will provide you with a clear concept. 

 

When "a" is negative it is called a Reflection (Vertical Reflection)

 

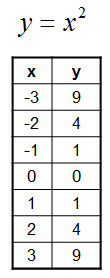
X-Intercepts or Zeroes 

 

 

When finding the x-intercept we must always think of the x co-ordinate as (x,0). Thus, y is

zero in the equation  y = a(x - h)² + k making it easy for us to isolate x. 

 

An example here is: y = a(x - 4)² - 6

 

0 +16 = (x - 3)² -16 +16   

 

√16 = √(x - 3)² 

 

±4 +3 = x - 3 +3 

 

x = 1 or x= 7          → This will be your two x-intercepts on the graph 

 

Step Pattern

Before heading on any further we must take a look at the step patern.

In every parabola there is a step pattern in which they follow the rule: as we go

left each time we have to square the number of times we go left to get the

number of square to go up adn vice versa for the right side.  The "a" value alters

this rule as it increases or decreases it. So if "a" is 2 then we have to double the

square so: 1 left and 2 up and then 2 left and 8 up. If "a" is 0.5 then it is: 1 left and

0.5 up 2 left and 2 up and vice versa on the right side.

 

Look at the video below if you need assistance